by Maggie,Foresight Ventures
PPT Link: https://img.foresightnews.pro/file/ProofRecursion.pdf
Good afternoon, everyone. Welcome to the tech talk.
My name is Maggie. I am the tech lead at Foresight Ventures.
I’m also thrilled to have Dr. Cathie as my co-speaker for today’s event. Dr. Cathie is the researcher of ZKML from the Privacy and Scaling Explorations Team of the Ethereum Foundation
We are excited to present you with a cutting-edge topic: “Proof Recursion and Its Practical Use in ZKML.”
Nowadays, proof recursion is almost the only way for zero-knowledge proof to prove huge and complicated statements. Additionally, ZKML brings verifiable AI onto the blockchain.

Now I’d like to start by briefly introducing our company.
- Foresight Ventures is a research-driven powerhouse in the field of crypto investment and incubation. Our comprehensive product matrix includes several key components.
- Firstly, Foresight News — the largest multilingual web3 media platform in the Asia-Pacific region
- Secondly, we proudly operate Foresight X, an accelerator program that is currently hosting a hacker house event.
- And finally, we have OpenBuild, a thriving global developer community.
If you would like to learn more about us, please don’t hesitate to visit our official websites or connect with us on our social media channels.

Now, let’s proceed to today’s agenda.
Our discussion will be divided into two parts: the “proof recursion” part and the ZKML part.
I will take the first half hour to explain why proof recursion is important, the evolution of the theory, and innovations based on folding schemes.
And then, Dr. Cathie will take over from there to introduce how proof recursion is used in practical ZKML

So, why do we care about proof recursion? This is started by the two challenges we faced when using ZKPs to prove program computations.
First of all, it is inefficient and impractical to prove very large and complex programs in a single monolithic ZKP. Looking at the diagram on the slide, we first need to transform the target program into arithmetic circuits or constraints, which ZKP can understand. Then we can feed these circuits and witness into ZKP proving systems to generate a proof, then later verification. Programs with extensive computations or complex algorithms can result in large circuits and numerous constraints. This increases the computational resources required for generating proofs. Sometimes, the memory constraint of the prover may even prevent the successful execution of the proof generation process. Additionally, some of the proofs are not applicable for blockchain verification, as there are gas limitations on the blockchain. So, controlling the size of the proof and the complexity of the proof verification process is also critical.

To address these challenges, we typically have three methods: proof composition, proof aggregation, and proof recursion
- Proof composition uses different proving systems one after another to generate the final proof. The first proving system is a fast prover but maybe it results in a large proof. To reduce the proof size, we can run the second system, which maybe is a slower prover but results in a shorter proof. This second proving system will prove that the verifier of the first system would accept the witness. So with proof composition, we can build a fast proving system, and the proof size is also small.
- The second method is proof aggregation. Proof aggregation is to aggregate multiple proofs into a single proof. For example, zkEVM consists of plenty of different circuits, like EVM circuits, RAM circuits, storage circuits, and so on. In practice, it is really expensive to verify all those proofs on the blockchain. So instead, we use proof aggregation, that is, use one proof to prove those multiple sub-circuit proofs are valid. This proof is much easier to be verified on blockchains.

- The third powerful method is proof recursion. The concept behind proof recursion is to build a chain of verifier circuits, where at each step, we can generate a proof that is much easier to be verified than the previous one. And at the end, we only need to verify the final proof with the least complexity.

Proof recursion can be used to realize Incrementally Verifiable Computation (IVC).
Consider a long computation done by iterating a function F. For example, we have an initial state S0, after performing F, we get S1, and we do it repeatedly to get the final output Sn. We want to prove that the output Sn is the correct result.
What proof recursion can do here is that we can incrementally update a proof i to a proof i +1. The proof is incrementally updatable, finally, we just need to verify one proof to make sure the whole execution chain is valid. So, It is most applicable in long computations and evolving computations.
- For the long computation, we can break it into steps and prove them by using IVC, which gradually reduces the need for memory for the prover.
- It is also valuable when applying the method in blockchains. As the state of a blockchain is constantly growing, with IVC prover, we can verify the current state by checking the latest recursive proof. If that proof is valid, we can believe the whole execution history is correct.
In conclusion, because of the limitation of the prover’s memory and timing, proof recursion is almost the only way we can prove very complicated statements. And, IVC is already used in succinct blockchains like Mina, VDF functions, ZKML, and so on.

In the past years, IVC has experienced three stages of evolution.
- The first one is based on SNARKS.
- The second is based on SNARKS or NARKS with accumulation.
- The latest one is based on the folding scheme. Which drives a lot of attention nowadays
Today, we will briefly review the first two types, then we will focus on the last one which is based on folding schemes.

- SNARK-based IVC is simple; the IVC prover needs to prove two things in each step.
- The iterate function F is correctly performed to produce the state S.
- And the proof π generated by the previous step is valid.
- So the recursive circuit embedded a snark verify circuit and fully verifies the proof generated by the previous step. This circuit is huge and costly.
- When it comes to the second type IVC, which is based on SNARKs with accumulation, like halo, and halo2, they don’t have to embed the SNARK verification circuit anymore. Instead, they introduced an accumulation scheme to defer the expensive part of the verification to an accumulator. And keep a small accumulation verifier in the recursive circuit. The cost of the accumulation verifier is much less than that of a full SNARK verifier.

The most up-to-date stage of IVC is based on folding schemes.
The folding scheme is first introduced by Nova. It is a method to compress two instances into one. Consider that we have a circuit C, and two instances (x1,w1) (x2,w2). We would like to fold them together and output a new folded instance (x, w).
If the two original instances are valid, we will end up with a valid folded instance. And if the folded instance is valid, the prover must know the valid witness w1 and w2 for original instances x1 and x2.

Now, Let’s try to fold two R1CS instances to see if we could meet the condition mentioned in the last slide.
We have two original witnesses, z1 and z2. z1 satisfies the equation Az1 * Bz1 = Dz1, indicating that it is a valid witness. Similarly, z2 is also a satisfying witness.
Then we fold them together using a random linear combination, setting z = z1 + a random number r * z2. We want the folded witness z is also a valid instance. This means that we want Az * Bz = Dz.
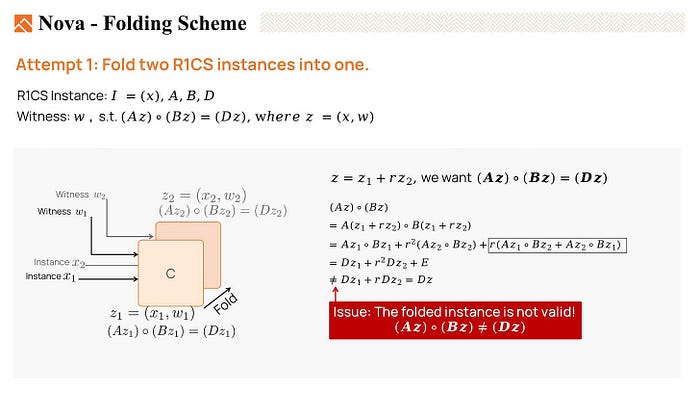
But, when we expand AzBz*, many cross terms are generated, and the result is not equal to Dz. Thus, z is not valid. We failed to fold two R1CS instances.

However, it could be equal if we allow some noises in the equation. Nova introduces an error vector E which absorbs the cross terms generated by folding. And a scalar c to absorb an extra factor of Dz.

This variant of R1CS is called relaxed R1CS. The instance includes x, a scaler c, and an error term vector E. And we’ll say that a valid witness Z satisfies Az * Bz = C * Dz + E.
Once again, we have two instances: (x1, c1, E1) with the witness w1, and (x2, c2, E2) with the witness w2. Both witnesses are valid. Now, Let’s see if we can fold them together.
We expand the equation Az * Bz. At last, we obtain c * Dz + E. So Z satisfies the equation, which is a valid witness.
Now, we can fold z1 and z2 to obtain a new folded witness, z, which is valid for ABD.

However, it is important to note that the error term E is derived from E1, E2, and T, where T is generated from the witnesses. Therefore, the folding prover must provide the witnesses to the verifier in order to compute E. This makes the folding scheme not non-trivial and also not zero-knowledge.
Being not non-trivial means that verifying the folded instance maybe not be more efficient than verifying the original two instances or the communication cost is too large. And not zero-knowledge is because the verifier has the knowledge of the witnesses in this scenario.

Now, what we can do is replace E and T with the commitments of E and T. Instead of sending the witnesses to the verifier, the prover sends commitments to help the verifier in computing.

So we replaced E with a short commitment to E in the instance and moved E to the witness. This is called committed-relaxed R1CS. Please note that to make it easier to understand, the method shown here was simplified from Nova’s paper.
Now, let’s go through the folding method. We have a folding prover and a verifier. The prover has two committed relaxed R1CS instances I1, I2 with witnesses z1, and z2. The verifier only has instances I1 and I2.
- At first, the prover would calculate the cross terms T, and send the commitment T to help the verifier to compute the folded instance.
- Then the verifier chooses a random r and sends it to the prover, we can use Fiat-Shamir transform to make it non-interactive.
- The folding prover computes the folded instance I and the witness Z.
- Verifier using the commitment to T and the original Instances I1, and I2, easily computes the folded instance I.
If two original witnesses z1 z2 are satisfying witnesses, then the folded witness z is a satisfying witness for the folded instance I. What we need to pay attention to here is that the commitment scheme must be additively holomorphic.

In IVC, we can use the folding scheme to fold the committed relaxed R1CS instances generated in each step.
We can fold the instances I0 and I1 to produce a folded instance I 0 to 1, we also call it the running instance. Then fold the new instance I2 with that running instance to get the I 0 to 2. We repeat the steps and get the final instance I 0 to n-1.
Finally, with the folded witness, we can generate proof for the final folded instance, then verify it.
However, this proof is imperfect because the SNARK verifier here only knows the witness is valid but cannot guarantee that the folding process has been done correctly.

So we have to verify the folding in each step.
We describe a function F’, the IVC recursive function, which includes both the iterate function F, as well as functions that can verify the folding process.
To verify the folding procedure, we first verify the hi, which is the hash of the folding result of the previous step. Then we verify the folding process that folds the instance i with running instance 0 to i-1 produces a new instance 0 to i is correct. And output the hi+1 which is the hash of the folding result. So we verified the folding process at each step with a very low cost by performing some hashes and some multiplications.

In conclusion, as we mentioned earlier, SNARK-based IVC is costly and inefficient as we need to read the whole proof and run the full verifier in the IVC recursive function.
When it comes to SNARKs with accumulation-type IVC, we still need to read the entire proof in each step. But what has improved is we can split the verification into a hard part and an easy part, running the easy part on the chain and deferring the hard part verification.
With folding-based IVC, all we have to do is to read the unproven instances and fold them into a running instance. The verification of the folding procedure is as simple as doing some basic hashing and multiplications. We can even defer the proving part to the last step.
Compared with the first two methods, folding-based IVCs incur the lowest recursion overhead. Therefore, they are the most optimized method at the current stage

After the introduction of Nova’s folding scheme, we’ve seen a whole bunch of different folding-based IVCs since last year.
SuperNova is one of them, which supports multiple types of functions in the IVC chain.
Given several non-deterministic functions, for example, F1 to F3, and a phi function pick one at each step. So we have 3 kinds of functions in the IVC chain, and each one may appear multiple times.
To fold these non-uniform IVC circuit instances. SuperNova applies Nova to each set of Fi separately. Using the ϕ function to pick out the running instance, and fold the current instance into the running instance. In this way, we fold each set of Fi separately

Another work is Sangria. Sangria is a folding scheme for Plonk, or more accurately, for PLONKish.
PLONKish offers greater flexibility in defining constraints and gate behaviors. It supports not only addition and multiplication constraints but also supports copy constraints and custom gate constraints, such as lookup constraints, which enable zk-unfriendly functions to be precomputed for better performance PLONKish is powerful, and it accelerates the ZK transformation of various programs. Sangria finds that the folding scheme can be easily expanded to the PLONKish arithmetic system. Supports addition and multiplication constraints, copy constraints, and degree 2 custom constraints.

In conclusion, proof recursion is a very smart technique that empowers us to prove huge and complicated statements.
And folding-based IVC schemes draw significant attention nowadays and are more efficient than SNARK-based IVCs. We believe they will be widely adopted in the industry.
The chart here listed the important innovations of folding-based IVC, let’s quickly go through it again.
- Nova, a folding scheme for R1CS, allows us to perform an IVC where the same function is repeatedly evaluated.
- And it would be better if we can perform different functions at each step. So SuperNova generalizes Nova to a non-uniform IVC, we can have several kinds of functions in the IVC chain, and each one may appear multiple times.
- And Sangria recognizes that Nova’s folding scheme can be applied to the PLONKish constraint system. It supports copy constraints and degree 2 custom constraints but does not support high-degree custom gates and lookup constraints in PLONKish constraint system.
- HyperNova introduces a multi-folding scheme for Customizable Constraint Systems (CCS), which is a generalization of R1CS. HyperNova supports high-degree custom gates and lookup constraints and uses the sum-check protocol to avoid quotients and FFTs(Fast Fourier Transforms).
- ProtoStar further enhances the folding scheme by supporting high-degree custom gates, lookup constraints, and non-uniform IVC.

Before ending my presentation, I’d like to emphasize that if anyone here has brilliant ideas and require resources to bring them to life, please don’t hesitate to reach out to us at Foresight Ventures.
Additionally, we invite you to join the second cohort of our Foresight X incubation program. We are here to support and nurture your entrepreneurial journey. With our deep industry know-how and ample resources, we will make sure your projects thrive.
Also, if you’re in the academic or research field, Foresight X offers competitive grants to support your research path.
And don’t forget, we’ve included a QR code here that integrates all links you may be interested in, including research reports.
Feel free to take a photo or scan the code to find out more, and if you have any questions after the session, you can find me on Twitter.
Thanks once again for joining us. Now, I’ll hand over the stage to Dr. Cathie for the next part.
Thanks to Mr. Keep for reviewing and refining the content.


