by Alan Lin, CTO of Fox Tech, and Sputnik Meng, Chief Scientist of Fox Tech
Almost all the problems encountered at zkRollup and zkEVM circuits are algorithmic in nature. The main reason why ZKP hardware acceleration is often mentioned is that algorithms are generally slow. In order to avoid falling into the “Algorithm is slow, only reply on hardware” awkward situation, we should from the essence of the algorithm to solve the problem. The key to solve this problem is to design an exquisite recursive proof scheme.
As smart contracts continue to evolve and more and more web3 applications come out, traditional Layer1 transactions such as Ethereum are rapidly increasing and congestion may occur at any time. How to obtain higher efficiency while ensuring the security provided by Layer1 becomes an urgent problem to be solved.
For Ethereum, zkRollup uses a zero-knowledge proof algorithm as an underlying building block to move expensive calculations that would otherwise need to be performed on Layer1 off the chain and provide proof of correctness of execution up the chain. The track features StarkWare, zkSync, Scroll and Fox Tech.
In fact, in the design of zkRollup, there is a high requirement for efficiency: you want to submit proof values that are small enough to reduce the computation of Layer1. In order to obtain a small enough proof length, various zkRollup projects are improving the algorithm and architecture design. For example, Fox developed its own proof algorithm FOAKS by combining the latest zero-knowledge proof algorithm to obtain the optimal proof time and length.
In addition, in the stage of verification, the most trivial means is the linear generation of proof and verification in turn. In order to improve efficiency, many proofs are packaged into one Proof, which is commonly referred to as Proof Aggregation.
Directly speaking, the verification of zkEVM generated proofs is a linear process. The Verifier needs to verify each generated proof in turn. However, this verification method has low efficiency and high communication overhead. For zkRollup scenario, higher verifier side overhead means more Layer1 calculation, which will lead to higher Gas fee.
Let’s start with an example: Alice wants to prove to the world that she went to Fox Park from the 1st to the 7th of this month. To this end, she could take a photo in the park with the newspaper of the day on each day from 1st to 7th, and the seven photos would be packaged as a proof.
In the above example, putting the seven photos directly into an envelope is an intuitive aggregation of proofs, which in practice corresponds to concatenating different proofs together and verifying them linearly in sequence, that is, verifying the first proof, then the second proof and subsequent proofs. The problem is that this does not change the size of the proof, nor does it change the duration of the proof, which is the same as proving and verifying one by one. To achieve logarithmic compression, use the Proof Recursion mentioned below.
Halo2 and STARK use the proof recursion scheme
To better illustrate what recursive proof is, let’s go back to the above example.
Alice’s 7 photos are actually 7 proofs. Now consider combining them, so Alice can take the picture at 1, take the picture at 2 with the newspaper at 2, and take the picture at 3 with the photo at 2 and the newspaper at 3. By the same token, Alice took the last photo on 7th with the photo of 6th and the newspaper of 7th, while the other partners could verify that Alice went to the park from 1st to 7th when they saw the last photo of 7th. As you can see, the previous seven proof photos have been condensed into one. A key trick in this process is the “photo with photo”, which is a recursive nesting of previous photos into later photos. It’s not like putting a lot of pictures together and taking a picture.
zkRollup’s recursive proof technique can drastically reduce proof size. To be specific, each transaction will generate a proof. Let’s assume that the original transaction calculation circuit is C0, P0 is the correctness proof of C0, V0 is the calculation process to verify P0, and the Prover converts V0 into the corresponding circuit, denoted as C0 ‘. At this time, for the proof calculation process C1 of another transaction, the circuit of C0 ‘and C1 can be combined. In this way, once the correctness of the combined circuit is verified, the proof P1 is equivalent to the correctness of the above two transactions at the same time, that is, the compression is realized.
By reviewing the above process, it can be found that the principle of compression lies in transforming the process of verification and proof into a circuit, and then generating “proof of proof”. Therefore, from this perspective, it is an operation that can recurse downward continuously, so it is also called recursive proof.
Halo2 and STARK’s Proof Recursion scheme can generate proofs in parallel and combine multiple proofs so that one proof can be validated for multiple transactions at the same time, reducing the computational overhead and greatly improving the efficiency of the system.
However, such optimization is still at the level above the specific zero-knowledge proof algorithm. To further improve efficiency, we need further optimization and innovation. FOAKS algorithm designed by Fox does this by applying the idea of recursion inside a proof.
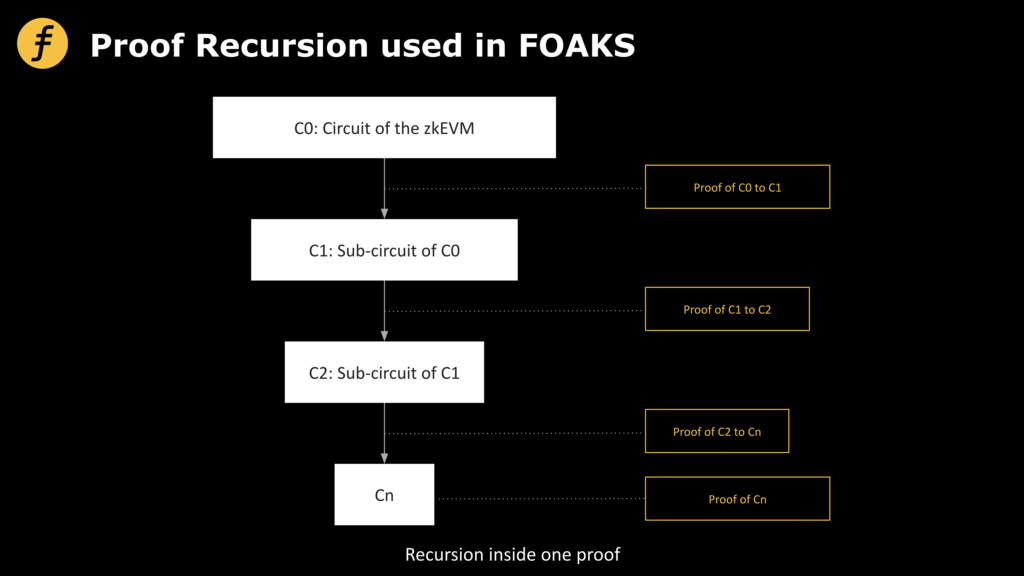
The proof recursion scheme used by FOAKS
Fox Tech is a zkEVM-based zkRollup project. In its proof system, the same technique of recursive proof is used, but the connotation is different from the above Recursion. The main difference is that Fox uses the idea of recursion inside a proof. In order to convey the core idea of Fox’s recursive proof, which involves reducing the problem to be proved over and over again until the reduced problem is simple enough, we need another example.
In the above example, Alice proved that she went to Fox Park one day by taking photos, so Bob put forward different suggestions. He believed that the problem of proving that Alice had been to the park could be reduced to proving that Alice’s mobile phone had been to the park, and the proof could be reduced to proving that Alice’s mobile phone was located in the park. Therefore, in order to prove that Alice has been to the park, all she has to do is send a location with her mobile phone while she was in the park. In this way, the size of the proof is changed from a photograph (a very high dimensional data) to a three dimensional data (latitude and longitude and time), effectively saving costs. This example is not entirely appropriate, because one might argue that Alice’s phone visit to Fox Park does not mean that Alice herself visited, but in practice the reduction is mathematically rigorous.
In particular, Fox’s use of recursive proof is recursion at the circuit level. In a zero-knowledge proof, we write a circuit of the problem we want to prove, and then use the circuit to calculate some equations that need to be satisfied. And instead of showing that these equations are satisfied, we write these equations into circuits again, and so on, until finally the equations that are satisfied are simple enough that we can easily prove them directly.
As you can see from this process, this is closer to the meaning of recursion. It is worth mentioning whether all algorithms can use this recursion technique, assuming that each recursion will turn the complexity of O(n) proof into an O(f(n)) proof, and the computational complexity of the recursive process itself is O(g(n)), then the total computational complexity after recursion becomes O1(n)=O(f(n))+O(g(n)),twice thenO2(n)=O(f(f(n)))+O(g(n))+O(g(f(n))),triple thenO3(n)=O(f(f(f(n))))+O(g(n))+O(g(f(n)))+O(g(f(f(n)))),…,And so on. Therefore, only functions of f and g corresponding to the algorithm property satisfy Ok(n)< for some k; O(n), this recursion technique is effective. In Fox, this recursive technique is effectively used to compress the proof complexity.
Conclusion:
The complexity of proof has always been one of the most important keys in zero-knowledge proof applications. The complexity of proof will become more and more important as the things to be proved become more and more complex, especially in huge ZK application scenarios like zkEVM, where the complexity of proof will have a decisive impact on product performance and user experience. Among many methods to reduce the complexity of final proof, the optimization of the core algorithm is the most important. Fox designed the exquisite recursive proof scheme on the basis of the most cutting-edge algorithm and used this technology to create the ZK-FOAKS algorithm that is most suitable for zkEVM, which is expected to become the performance responsibility of zkRollup.
Reference literature:
https://blog.csdn.net/weixin_44383880/article/details/126338813



