Written by: Ivan Lin, CTO of Fox Tech, and Sputnik Meng, Chief scientist of Fox Tech

preface

The computational agent idea between Prover and Verifier is one of the core content of zero-knowledge proof. It is a tool to balance complexity trade-off between prover and verifier workload. The essential difference of different zero-knowledge proof algorithms lies in the different degree of computing agent; A high degree of proxy makes the calculation of verification easy, but it may make the complexity of proof high, resulting in a long proof time, or the size of the generated proof is large. On the contrary, a low degree of proxy will make the verifier more expensive.

Figure 1: Effect of computational agent degree on zero-knowledge proof

What is a computing agent

With the expansion of applications and users on Ethereum, the degree of congestion on Ethernet mainnet keeps increasing, and using zkRollup for Layer2 expansion becomes a very attractive scheme. FOX is the project that focuses on using FOAKS algorithm for zkRollup. The feasibility of zkRollup essentially lies in the principle feasibility of the zero-knowledge proof algorithm used. In simple terms, the function of zero-knowledge proof algorithm is to make the prover prove something to the verifier without revealing any information about it. zkRollup is constructed to take advantage of this property, allowing Layer2 nodes to perform computations that would otherwise be done in Layer1, while providing a proof of correctness to the Layer1 node.

In a broader sense, the above process can be understood as that, due to the limited computing capacity of the verifier (Layer1 node), the computation of this part is delegated to the prover (Layer2 node). The prover completes the task and needs to return the result to the verifier. From this point of view, we can say that the zero-knowledge proof algorithm enables the realization of a “computational agent” that guarantees correctness. In the macro sense, this kind of computing agent example can be represented in the form of zkRollup application, and in the specific zero-knowledge algorithm, this kind of computing agent idea has various applications.

This article focuses on the validation calculations that FOAKS uses for Code-Switching, mentioned in Orion, to make the prover help the verifier perform, and how FOAKS applies this technique to recursion. This reduces the size of the proof and the overhead of the verifier.

Why do you need to compute agents

From the practical point of view of the system, the computing power of the computing node is limited in many cases, or the computing resources are very precious. For example, all calculations on the Layer1 chain (including transfers and contract calls) need to be agreed upon by all nodes, and users have to pay high fees for this. Therefore, in this case, it is natural to “delegate” the computation that would otherwise be handled by the consensus node to the nodes down the chain, to avoid consuming the resources on the chain. This is the kind of off-chain computing that FOX is focusing on.

From the perspective of cryptography theory, in the GMR model, the prover is limited to have infinite computing power and the verifier has polynomial computing power. If the verifier also has infinite capacity, then the basic property of zero-knowledge proof cannot be satisfied. So naturally, tilting the computation in favor of the prover, making the prover take on more computation is a problem that many zero-knowledge prover algorithms design.

Of course, in order to achieve this, we need special skills.

Code Switching

This section describes the Code Switching techniques used in Orion. Both Orion and FOAKS use Brakedown as a polynomial commitment scheme, and Code Switching is a process named in Orion in which a prover performs validation calculations in place of a verifier.

In Understanding Brakedown, the Polynomial Commitment Protocol in FOAKS, we described how the verifier’s verification is calculated as follows:

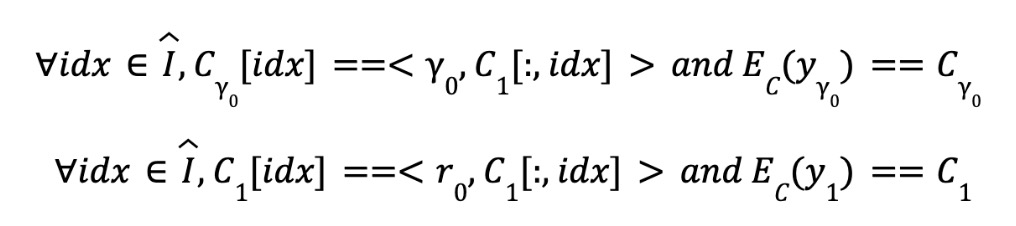
Now if you make the prover undertake this part of the calculation, the prover will perform the calculation and attach the proof value to prove that his calculation is correct.

This is done by writing the same equation as R1CS circuit:

The computing agent in FOAKS

A similar technique is used to compute agents in FOAKS, where it is worth noting that FOAKS implements non-interactive proofs thanks to the Fiat-Shamir heuristic technique. For more information, refer to the Fiat-Shamir Heuristic! How to Transform Interactive Proofs into Non-Interactive Proofs! . So FOAKS ‘challenge generation is different from the code-switching method used by Orion, with a new equation added to the circuit:

Then the prover in FOAKS also generates computational proofs that are validated by the proxy verifier. For the verification process, FOAKS uses the algorithm itself to iterate, which is also the key content of FOAKS recursion. For details, see How to Design an Excellent Proof Recursion Scheme.

Through a certain number of iterations, the size of the proof can be compressed, thus greatly reducing the computational burden and communication complexity of the verifier. This is the significance of the zero-knowledge proof scheme FOAKS to the zkRollup of FOX.

conclusion

The degree of computation proxy for the zero-knowledge proof algorithm used in zkRollup needs to be carefully designed and must be just right for it to achieve optimal overall efficiency. And FOAKS algorithm realizes the adjustable computation agent through recursion of its own iteration, which is a zero-knowledge proof algorithm specially designed for zkRollup.
Reference literature

1.Orion： Xie, Tiancheng, Yupeng Zhang, and Dawn Song. “Orion: Zero knowledge proof with linear prover time.” Advances in Cryptology–CRYPTO 2022: 42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, August 15–18, 2022, Proceedings, Part IV. Cham: Springer Nature Switzerland, 2022.