by Fox Tech CEO, Frederick Kang; Fox Tech CTO, Alan Lin
Foreword: The Ethereum Virtual Machine is a code operating environment built on the Ethereum blockchain. The contract code can be completely isolated from the outside and run inside the EVM. Its main function is to process smart contracts in the Ethereum system. The reason why Ethereum is Turing complete is that developers can use the Solidity language to create applications that run on the EVM, and all computable problems can be calculated. But only Turing completeness is not enough. People also try to encapsulate EVM in the ZK proof system, but the problem is that there will be a lot of redundancy when encapsulating. The “Small Table Mode” zkEVM invented by Fox will not only ensure that native Solidity Ethereum developers can migrate to zkEVM seamlessly, but will also greatly reduce the redundant cost of packaging EVM to the ZK proof system.
EVM is undergoing an epic ZK transformation since its inception in 2015. This major transformation has two main directions.
The first direction is the so-called zkVM track. This track project is dedicated to improving the performance of the Application to the optimum, and the compatibility with the Ethereum virtual machine is not the primary consideration. There are two sub-directions here. One is to make your own DSL (Domain Specific Language). For example, StarkWare is committed to promoting the Cairo language, which is not easy to promote. The second is that the goal is compatible with existing relatively mature languages. For example, RISC Zero is committed to making zkVM compatible with C++ and Rust. The difficulty of this track is that the constraints of the final output are more complicated due to the introduction of the instruction set ISA.
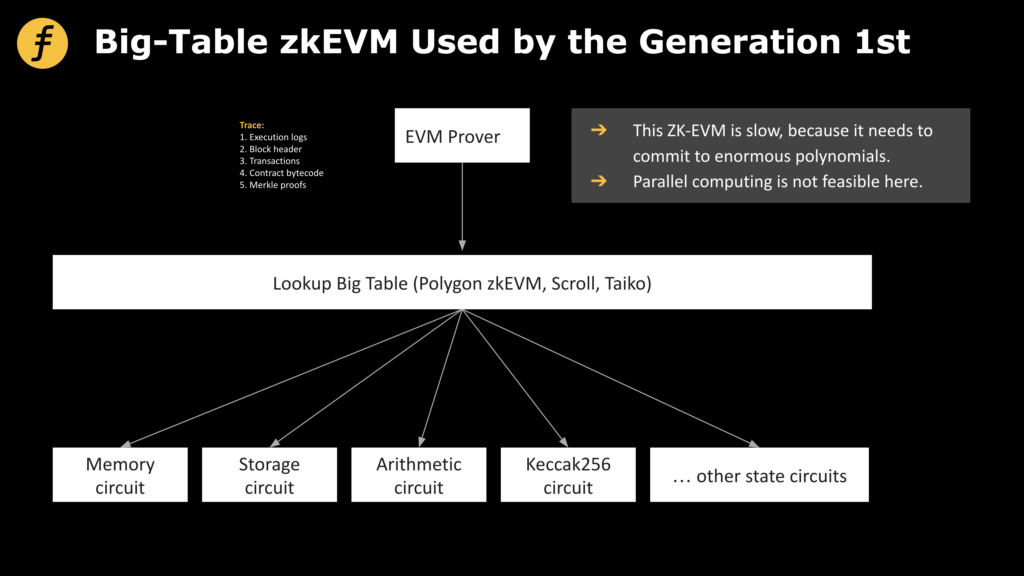
The second direction is the so-called zkEVM track. This track project is dedicated to the compatibility of EVM Bytecode, that is, EVM codes at the Bytecode level and above all generate corresponding zero-knowledge proofs through zkEVM, so that native Solidity Ethereum developers It will be possible to migrate to zkEVM at no cost. The players on this track mainly include Polygon zkEVM, Scroll, Taiko and Fox. The difficulty of this track is that it is compatible with EVM, which is not suitable for encapsulating redundancy costs in the ZK proof system. After a long period of thinking and argumentation, Fox finally found the key to fundamentally reduce the huge redundancy of the first generation zkEVM: “small table mode” zkEVM.
Data and proof circuits are the two core elements of zkEVM to generate proofs. On the one hand, in zkEVM, the prover needs all the data involved in the transaction to prove that the state transfer brought about by the transaction is correct, while the data in EVM is large and complex in structure. Therefore, how to organize and organize the data required for the proof is a problem that needs to be carefully considered to build an efficient zkEVM. On the other hand, how to efficiently prove (or verify) the validity and correctness of calculation execution through a series of circuit constraints is the basis for ensuring the security of zkEVM.
Let’s talk about the second question first, because this is a question that all teams that design zkEVM need to consider. The essence of this question is actually “what do we want to prove?” At present, everyone’s thinking on this question is similar, because A transaction (or the op-code it involves) may be diverse, and it is unrealistic to directly prove that the state changes brought about by each step of the operation are correct in sequence, so we need classification proofs.

For example, we put together each change of elements in the stack, specially write a stack circuit proof, write a set of arithmetic circuits for pure arithmetic operations, and so on. In this way, the situations that each circuit needs to consider become relatively simple. These circuits with different functions have different names in different zkEVMs. Some people call them circuits directly, while others call them (sub)state machines, but the essence of the idea is the same.
In order to explain the meaning of doing this more clearly, let us give an example, assuming that we now want to prove the addition operation (take out the upper 2 elements of the stack, and put their sum back to the top of the stack):
Suppose the original stack is [1,3,5,4,2]
Then if we do not classify and split, we need to try to prove that the stack becomes [1,3,5,6] after the above operations.
And if the classification is split, we only need to prove the following things separately:
stack circuit:
C1: Prove that [1,3,5,4,2] becomes [1,3,5] after popping out 2 and 4
C2: Prove that [1,3,5] becomes [1,3,5,6] after push(6)
Arithmetic circuit:
C3: a=2, b=4, c=6, prove a+b=c
It is worth noting that the complexity of the proof is related to the number of situations that the circuit needs to consider. If it is not classified and split, the possibility that the circuit needs to be covered will be huge.
Once the classification is split, the situation of each part will become relatively simple, so the difficulty of proof will be significantly reduced.
But classification and splitting will also bring about other problems, that is, the data consistency problem of different types of circuits. For example, in the above example, we actually need to prove the following two things:
C4: “the number popped in C1” = “a and b in C3”
C5: “the number of pushes in C2” = “c in C3”
In order to solve this problem, we return to the first question, that is, how do we organize the data involved in the transaction, and we will discuss this topic next:
An intuitive method is this: through trace, we can disassemble each step involved in all transactions, know the data involved, and send a request to the node to obtain the part of the data that is not in the trace, and then we will It is arranged into a large table T as follows:
“First step operation” “Data involved in the first step operation”
“Second step operation” “Data involved in the second step operation”
…
“Operation nth step” “Data involved in operation nth step”
So, in the above example, we would have a line that records
“step k: addition” “a=2, b=4, c=6”
The above C4 can be proved as follows:
C4(a): The number popped by C1 is consistent with the kth step in the large table T
C4(a): a and b of C3 are consistent with the kth step in the large table T
C5 is also similar. This operation (to prove that some elements appear in a table) is called lookup. We will not introduce the specific algorithm of lookup in this article, but it is conceivable that the complexity of lookup operation is closely related to the size of the large table T. So now we come back to the first question: how to organize the data that will be used in the proof?
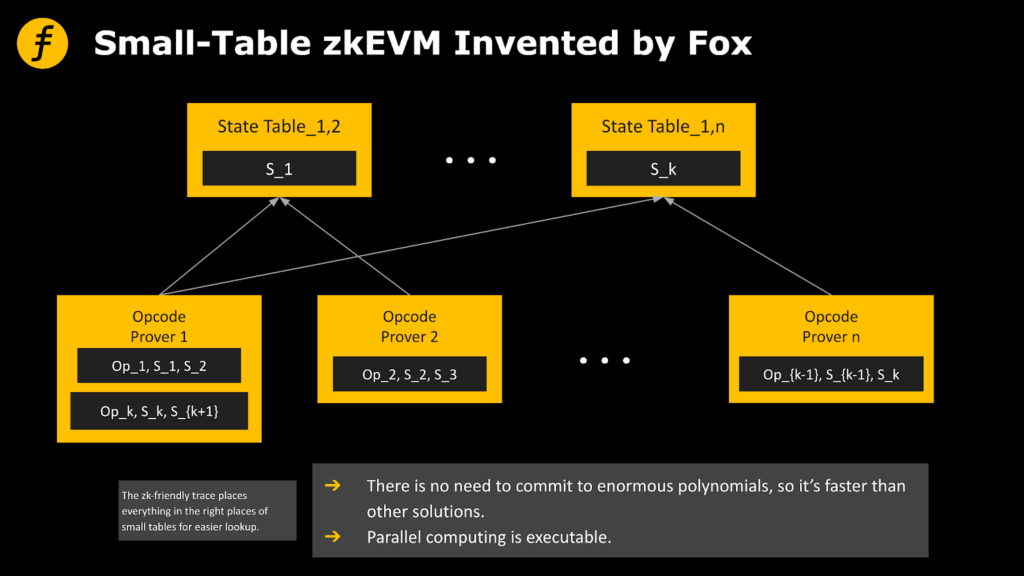
We consider the following series of table constructions:
Form Ta:
“first operation of type a” “data involved in the first operation of type a”
“The second operation of type a” “The data involved in the second operation of type a”
…
“The mth operation of type a” “The data involved in the mth operation of type a”
Form Tb:
“first operation of type b” “data involved in first operation of type b”
“second operation of type b” “data involved in second operation of type b”
…
“The mth operation of type b” “The data involved in the nth operation of type b”
…
The advantage of constructing multiple small tables in this way is that we can directly perform lookups in the corresponding small tables according to the types of operations involved in the required data. In this way, the efficiency can be greatly improved.
A simple example (assuming we can only lookup one element at a time) is that if we want to prove that the 8 letters a~h exist in [a,b,c,d,e,f,g,h], we need Perform 8 lookups on a table of size 8, but if we divide the table into [a,b,c,d] and [e,f,g,h], we only need to lookup these two Tables were looked up 4 times on it!
The design of this small table is used in the zkEVM of layer 2 of FOX to improve efficiency. In order to ensure complete proof in various situations, the specific small table splitting method needs to be carefully designed, and the efficiency improvement The key is to balance the classification of the content of the table with its size. Although implementing a complete zkEVM in this framework requires a huge amount of work, we expect that such a zkEVM will have a breakthrough in performance.
Conclusion: The “small table mode” zkEVM invented by Fox not only ensures that native Solidity Ethereum developers can migrate to zkEVM at no cost, but also greatly reduces the redundant cost of encapsulating EVM into the ZK proof system. This is a major change in the structure of zkEVM, which will have a profound impact on Ethereum’s expansion plan.



