Deeply Parse The Polynomial Commitment Protocol Brakedown In FOAKS

by Shuiyue Kang, CEO of Fox Tech, and Xuanji Meng, Chief scientist of Fox Tech

If cryptographers had not discovered the connection between Tensor Product and polynomial values, Brakedown, a polynomial commitment protocol, would have been hard to make. That would have made Orion based on Brakedown and new fast algorithms like FOAKS impossible.

In many zero-knowledge proof systems that rely on polynomial commitment, different commitment protocols are used. According to Justin Thaler of a16z in the August 2022 article “Measuring SNARK performance: Frontends, backends, and the future “evaluation, Brakedown although has a larger Proof Size, but is undoubtedly the fastest polynomial commitment protocol.

FRI, KZG, Bulletproof are the more common polynomial commitment protocols, but speed is their bottleneck. Plonky algorithm adopted by zkSync, Plonky2 algorithm adopted by Polygon zkEVM, and Ultra-Plonk algorithm adopted by Scroll are all based on KZG’s polynomial commitment. Prover involves a lot of FFT calculations and MSM operations to generate polynomials and commitments, both of which bring a lot of computational burden. While MSM has the potential to run multithreaded accelerations, it requires a lot of memory and is slow even at high parallelism, while large FFTS rely heavily on frequent shuffling of algorithm run time data and are difficult to load across computing clusters with distributed accelerations.

Thanks to Brakedown, a faster polynomial commitment protocol, the complexity of such operations is greatly reduced.

FOAKS, or Fast Objective Argument of Knowledges, is a Brakedown based framework of zero-knowledge proof system proposed by Fox Tech. FOAKS goes further than Orion in reducing FFT arithmetic, with the goal of eventually eliminating FFTS. In addition, FOAKS has devised a new and very elegant proof recursion to reduce proof size. The advantage of the FOAKS framework is that it has a small proof size while achieving linear proof time, which makes it ideal for zkRollup scenarios.

In the following sections, we describe in detail Brakedown, the polynomial commitment protocol used by FOAKS.

In cryptography, the Commitment protocol is promised to a secret value by the Prover to generate a public commitment value with Binding and Hiding. Later, the submitter needs to open the commitment and send a message to the verifier. To verify the correspondence between promises and messages. This makes the functions of commitment protocol and hash function have a lot in common, but the commitment protocol often relies on the mathematical structure of public key cryptography. And Polynomial Commitment is a kind of polynomial commitment scheme, in other words, the promised value is polynomial. At the same time, the polynomial commitment protocol also contains the algorithm to take the value at a given point and give the proof, which makes the polynomial commitment protocol itself become an important cryptographic protocol and the core part of many zero-knowledge proof systems.

The discovery of the connection between Tensor Product and polynomial values has led to a tensor product of which Brakedown is representative of a series of polynomial commitment protocols.

Before going into the details of Brakedown’s protocol, there are some basics. You need to understand Linear Code, collapse-resistant Hash functions, Merkle trees, Tensor products and Tensor Product representations of polynomial values.

First, Linear Code. A linear code of message length k and code word length n is a linear subspace C∈Fⁿ, such that there is an injective from message to a code word, called encoding, denotedE_C：F^k→C. Any linear combination of code words is still a code word. The distance between two code words u and v is their Hamming distance, denoted as △(u,v). The shortest distance is d=min_u,v△(u,v) . Such codes are denoted as [n,k,d] linear codes, and dn is used to represent the relative distance of codes.

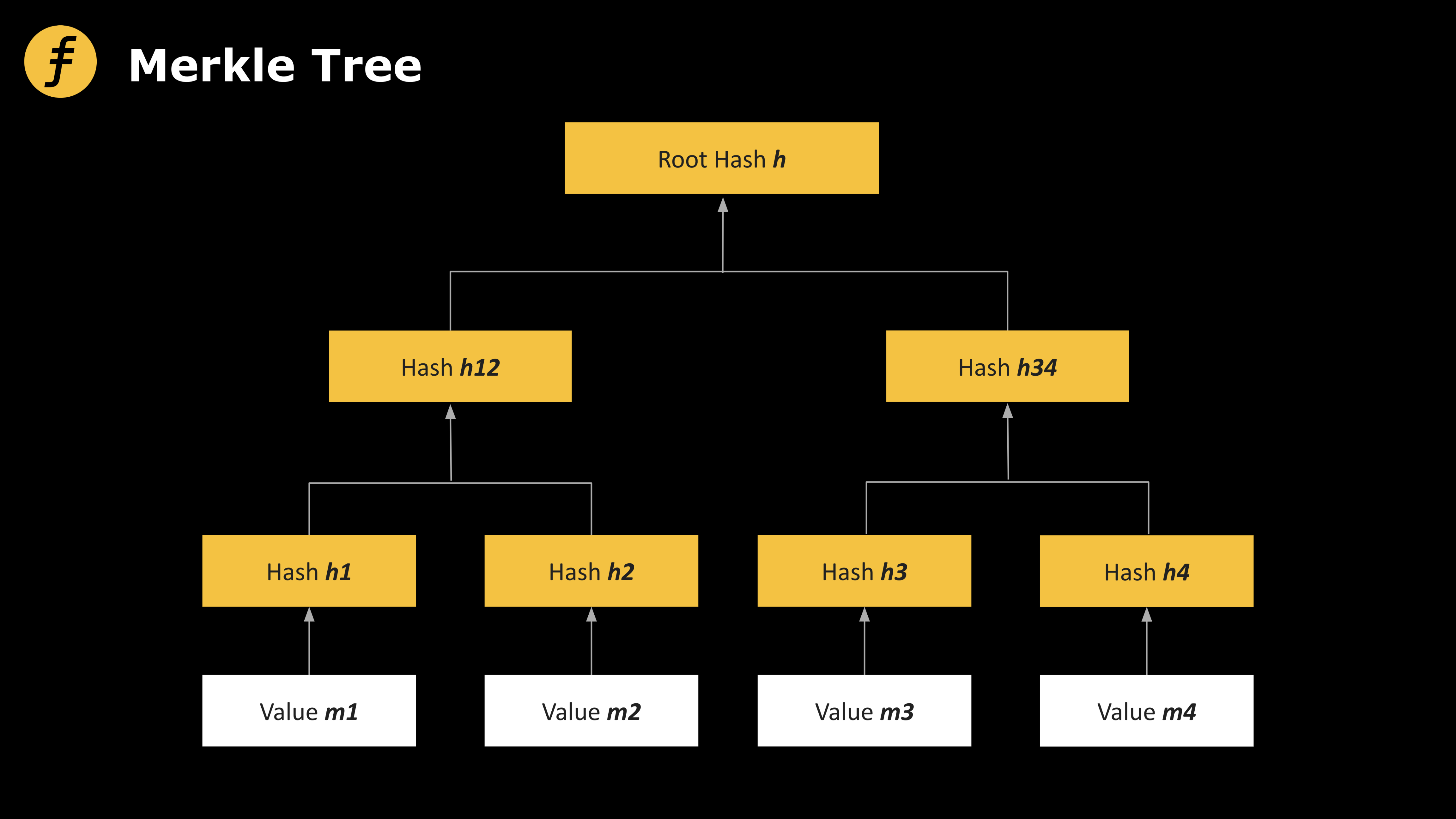
Secondly, anti-collision Hash Function and Merkle Tree.

Use H:{0,1}^2λ→{0,1}^λ to represent a hash function. The Merkle tree is a special data structure that can fulfill the promise of 2^d messages, generate a hash value h, and require d+1 hashes whenever any message is opened.

The Merkle tree can be represented as a binary tree with depth d, where L message elements m1,m2,… ,ml respectively correspond to the leaves of the tree. Each internal node of the tree is hashed by its two children. When the message mi is opened, the path from mi to the root node needs to be exposed.

Use the following notation to indicate:

1. 1. h←Merkle.Commit(m₁,…,m_l)
2. 2. (m_i,π_i)←Merkle.Open(m,i)
3. 3. {0,1}←Merkle.Verify(π_i,m_i,h)

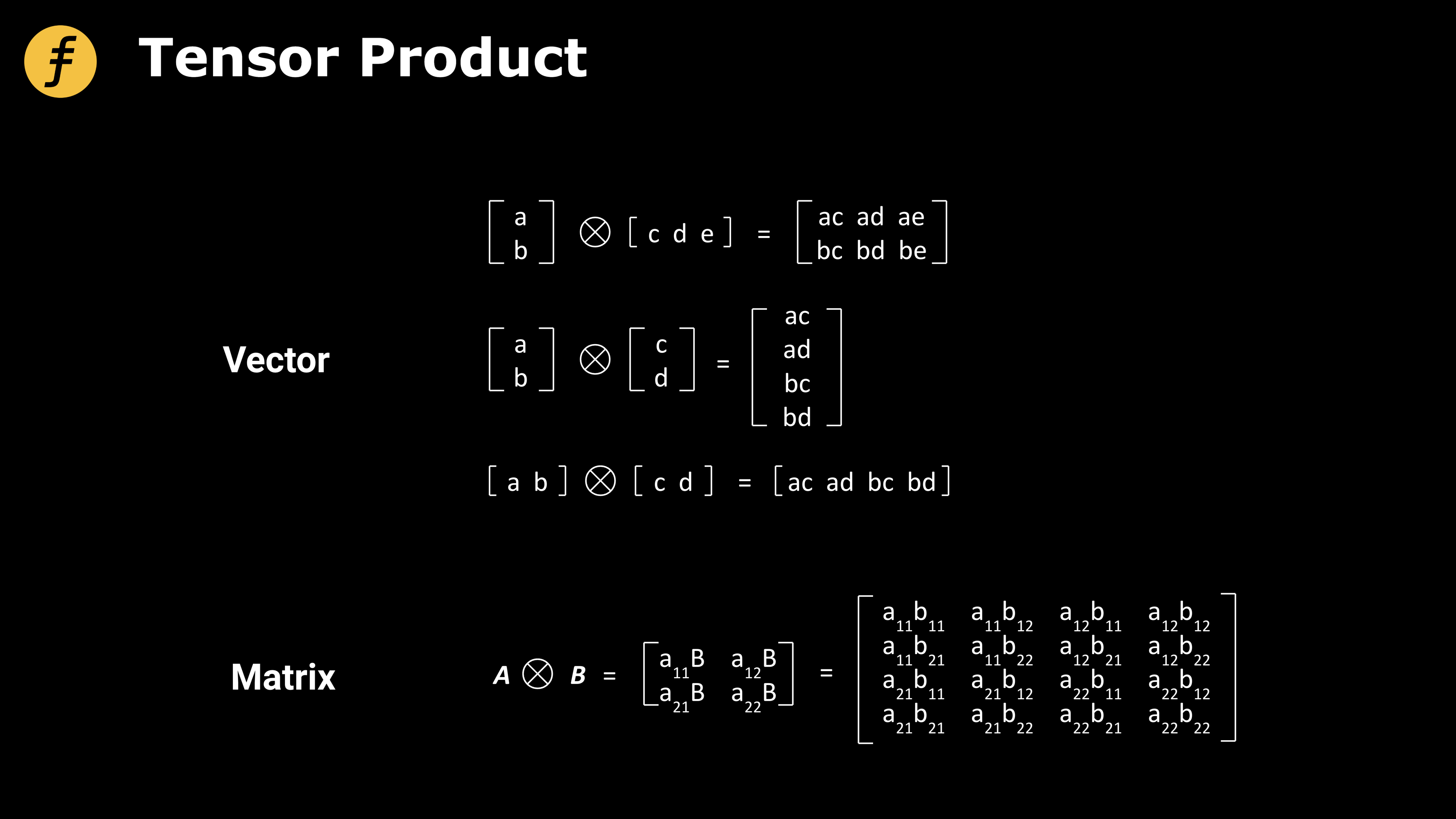
And we need to understand how the Tensor Product operation works. Mathematically, tensor is the extension of vector and matrix to higher dimensional space, which is a very important research object. Detailed discussion of tensor is beyond the scope of this paper. Here, only the tensor product operation of vector and matrix is introduced.

Next, we need to know the tensor product representation of polynomial values.

It is mentioned in [GLS+] that the values of polynomials can be expressed as tensor products. Here we consider the promise of multilinear polynomials.

Specifically, given a polynomial , the vector x₀,x₁,…,x_logN-1 value can be written as:

By the definition of multilinearity, each of these variables has a degree of 0 or 1, so there are N monomials and coefficients, and logN variables. Let

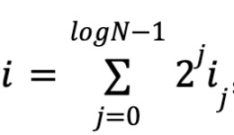
, where i₀i₁…i_logN-1 is the binary representation of i. Let w represent polynomial coefficients,

Let

,

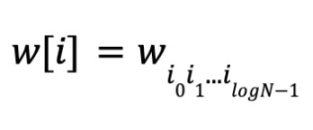
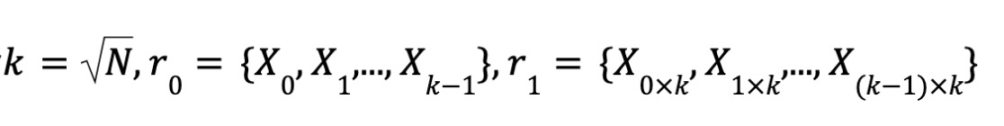
. So we have X=r₀⊗r₁。.

Thus, polynomial values can be expressed as tensor products: ϕ(x₀,x₁,…,x_logN-1)=<w,r₀⊗r₁>.

Finally, we look at the Brakedown process used in FOAKS, Orion[XZS22].

First, PC.Commit divides the polynomial coefficient w into the matrix form of kk and codes it (refer to the linear code in “Preparatory Knowledge”), denoting it C₂. A Merkle tree is then committed for each column of C₂[:,i], and another Merkle tree is then committed for each column formed at the Merkle tree root.

In the calculation of proof of value, two points need to be proved, namely Proximity and Consistency. The approximation ensures that the promised matrix is indeed close enough to the encoded code word. Consistency assurance y=<w,r₀⊗r₁> .

Approximation test: Approximation test consists of two steps. First, the verifier sends a random vector Y₀ to the prover, who computes the inner product of Y₀ and C₁ , that is, computes a linear combination of C₁ ‘s rows with the components of Y₀ as coefficients. Because of the nature of linear codes, C_y0 is the code word for Y_y0. After that, the prover proves that C_y0 is indeed computed from the promised code word. To prove this, the verifier randomly selects t columns, and the prover opens the corresponding columns and provides the Merkle tree proof. The verifier checks that the inner product of these columns and Y₀ is equal to the corresponding position in C_y0. It is shown in [BCG20] that if the linear code used has a constant relative distance, then the promised matrix is close to a code word with overwhelming probability (overwhelming probability means that the probability of a statement being true is negligible).

Consistency checking: The consistency checking and approximation checking procedures are exactly the same. The difference is, instead of using the random vector Y₀ , we use r₀ directly to do the linear combination part. Similarly, c₁ is a linear code for the message y₁ and has ϕ(x)=<y₁,r₁>. It is proved in [BCG20] that by consistency test, if the promised matrix is close to a code word, it is true with overwhelming probability y=ϕ(x).

In pseudo-code form, we give the Brakedown protocol flow:

Public input：The evaluation point X，parsed as a tensor product X=r₀⊗r₁;

Private input：The polynomial ϕ ，the coefficient of is denoted by w.

Let C be the [n,k,d]-limear code，E_C：F^kFⁿ be the encoding function，N=k×k. If N is not a perfect square，we can pad it to the next perfect square. We use a python style notationmat[:,i] to select the i-th column of a matrix mat。

1. 1. function PC. Commit(ϕ)：
2. 2. Parse w as a k×k matrix. The prover locally computes the tensor code encoding C₁，C₂ ，C₁ is a k×n matrix，C₂ is a n×n matrix.
3. 3. for i∈ [n] do
4. 4. Compute the Merkle tree root Root_t=Merkle.Commit(C₂[:,i])
5. 5. Compute a Merkle tree root R=Merkle.Commit([Root₀,……Root_n-1]),and output R as the commitment.
6. 6. function PC. Prover(ϕ, X, R)
7. 7. The prover receives a random vector Y₀∈F^k from the verifier
8. 8. Proximity
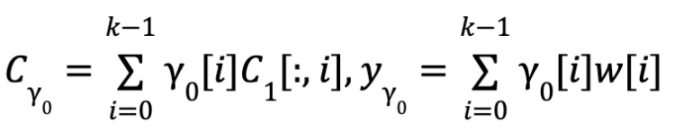
9. 9. Consistency
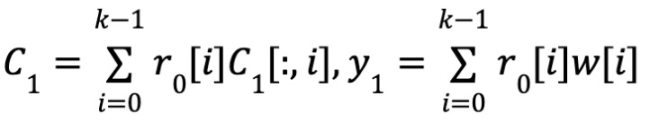
10. 10. Prover sends C₁,y₁,C₀,y₀ to the verifier.
11. 11. Verifier randomly samples t[n] as an array Î and send it to prover
12. 12. for idx∈Î do
13. 13. Prover sends C₁ [:,idx] and the Merkle tree proof of Root_idx for C₂ [:,idx] under R to verifier
14. 14. function PC. VERIFY_EVAL(π_X,X,y=ϕ(X),R)
15. 15. Proximity: ∀idx∈Î,C_Y0[idx]==<Y₀,C₁[:,idx]>and E_C(Y_y0)==C_Y0
16. 16. Consistency:∀idx∈Î,C₁[idx]==<Y₀,C₁[:,idx]>and E_C(Y₁)==C₁
17. 17. y==<r₁, y_1>
18. 18. ∀idx∈Î, E_C(C₁[:,idx]) is consistent with ROOT_idx, and ROOT_idx’s Merkle tree proof is valid.
19. 19. Output accept if all conditions above holds. Otherwise output reject.

Conclusion: Polynomial commitment is a very important cryptographic protocol, which is widely used in many cryptographic systems, especially zero-knowledge proof systems. This paper introduces the polynomial commitment Brakedown protocol and its related mathematics in detail. As an important underlying component of FOAKS, Brakedown plays an important role in improving the instantiation performance of FOAKS.

Reference literature:

1. [GLS+]:Alexander Golovnev, Jonathan Lee, Srinath Setty, Justin Thaler, and Riad S. Wahby. Brakedown:  Linear-time and post-quantum snarks for r1cs. Cryptology ePrint Archive. https://ia.cr/2021/1043.
2. [XZS22]:Xie T, Zhang Y, Song D. Orion:  Zero knowledge proof with linear prover time[C]//Advances in Cryptology — CRYPTO 2022: 42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, August 15-18, 2022, Proceedings, Part IV. Cham: Springer Nature Switzerland, 2022: 299-328.https://eprint.iacr.org/2022/1010
3. [BCG20]:Bootle, Jonathan, Alessandro Chiesa,  and Jens Groth. “Linear-time arguments with sublinear verification from tensor codes.” Theory of Cryptography:  18th International Conference, TCC 2020, Durham, NC, USA, November 16-19, 2020, Proceedings, Part II 18. Springer International Publishing, 2020.
4. Justin Thaler from A16zcrypto, Measuring SNARK performance: Frontends, backends, and the future
5. https://a16zcrypto.com/measuring-snark-performance-frontends-backends-and-the-future/
6. The introduction of tensor product: https://blog.csdn.net/chenxy_bwave/article/details/127288938